Combinaciones
Se llaman Combinaciones al número de grupos diferentes que se pueden formar con los elementos de un conjunto, de tal manera que en cada grupo:
- No importa el orden de colocación de los elementos.
- No entran todos los elementos del conjunto.
- Si los elementos no se repiten, se llaman Combinaciones ordinarias o simplemente Combinaciones.
- Si los elementos se pueden repetir, se llaman Combinaciones con repetición.
Combinaciones ordinarias
En las Combinaciones ordinarias no importa el orden de colocación de los elementos y estos no se pueden repetir. Se representan → Cm,n
Observamos que en cada equipo: No Influye el orden de colocación → Luis-Ana es el mismo que Ana-Luis. No se repiten → un alumno no se puede repetir en un equipo. No entran todos los alumnos → de cinco alumnos entran dos. Al cumplir estas condiciones son Combinaciones ordinarias → C5,2 = 10
Para encontrar una fórmula que nos ayude a calcular las Combinaciones ordinarias de m elementos tomados de n en n analizamos el caso anterior.
Si en cada uno de los 10 equipos formados cambiamos el orden de los dos amigos, (lo hacemos con permutaciones de 2, P2 = 2! = 2 x 1 = 2), obtenemos 2 equipos distintos, lo que nos daría un total de 10 x 2 = 20 equipos. Este resultado coincide con las V5,2 Por tanto →
C5,2 * P2 = V5,2 → C5,2 = V5,2 / P2 = (5x4) /(2x1) = 20 / 2 = 10
Esta fórmula se puede generalizar para m elementos tomados de n en n
Ejemplo A la vuelta de las vacaciones se reunen seis amigos, y se intercambian saludos entre todos. ¿Cuántos saludos se intercambiarán?.
- No importa el orden → Es igual que Luis salude a Ana que Ana a Luis.
- No se repiten los amigos → No se puede saludar un amigo a si mismo.
- No participan todos los amigos → De 6 participan 2.
Según los datos, son Combinaciones → C6,2 y el resultado es →
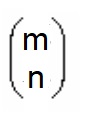equivale a Cm,n
= = 
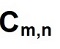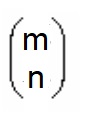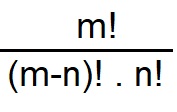
Combinaciones con repetición
En las Combinaciones con repeticióndos los elementos se pueden repetir y no influye su orden de colocación. Los grupos se diferencian en algún elemento. Se representan → CRm,n
Queremos saber las Combinaciones con repetición que se pueden formar
con los elementos del conjunto (A, B, C).
De orden 1 (con un elemento) (n=1) (m=3): Solo podemos formar A-B-C → (3)
CR3,1 = 3 que coinciden con las Combinaciones ordinarias C3,1 = 3.
Es decir CR3,1 = C3, 1 (Observamos que 3 = 3+1-1).
De orden 2 (con dos elementos) (n=2): Para formarlas hacemos lo mismo que con las Combinaciones ordinarias, con la diferencia de que como se pueden repetir los elementos tendremos que añadir a cada una de las combinaciones de orden uno,
el mismo elemento y todos los siguientes. AA-AB-AC-BB-BC-CC = (6) → CR3,2 = 6.
Este resultado coincide con las Combinaciones ordinarias con un elemento más (m=3+1=4) → C4,2 = 4x3/2 = 6. Es decir: CR3,2 = C4, 2 (Vemos que 4 = 3+2-1).
De orden 3 (con tres elementos) (n=3): Para formarlas hacemos lo mismo que en el caso anterior, añadiendo a cada una de las de orden dos el mismo elemento y todos los siguientes. AAA-AAB-AAC-ABB-ABC-ACC-BBB-BBC-BCC-CCC = (10) → CR3,3 = 10.
Este resultado también coincide con las Combinaciones ordinarias con un
elemento más (m=4+1=5) → C5,3 = (5x4x3)/(3x2) = 60/6 = 10.
Por tanto CR3,3 = C5, 3 (Observamos que 5 = 3+3-1)
Siguiendo este procedimiento, es fácil deducir la fórmula para generalizar el cálculo de las Combinaciones con repetición de m elementos tomados de n en n
Ejemplo ¿De cuántas formas podemos elegir tres pasteles en una pasteleria que tiene siete tipos distintos de pasteles?.
- No importa el orden → da lo mismo nata y crema que crema y nata.
- Sí se pueden repetir → podemos pedir 2 o 3 iguales.
- No entran todos los pasteles → De 7 tomamos 3.
-
Serán Combinaciones con repetición y el resultado es →
- CR7,3 = C7+3-1, 3 = C9, 3 = V9, 3/P3 = (9x8x7)/(3x2x1) = 504/6 = 84 formas.
Puede haber casos en que el número de elementos (n) de los grupos a formar tenga más elementos (m) de los que nos dan para formar dichos grupos. Es decir → n > m.
Ejemplo Queremos saber cuántas bandejas diferentes de cinco pasteles se pueden comprar en una pasteleria que solo tienen pasteles de tres tipos.
- No Influye el orden de colocación.
- Y se tiene que repetir algún pastel → n > m.
= (7x6x5x4x3) / (5x4x3x2x1) = (7x6) / (2x1) = 42 / 2 = 21 bandejas